Demonstration of Maya geometry
This page illustrates how the rules of Maya geometry differ from our everyday experience. Maya design operates under a specific grammar and syntax that must be recognized before the full meaning can be extracted. A single eccentric chipped from chert has been chosen to illustrate a wide range of design principles, but there are many more yet to be discovered and articulated.
Snake figure
(148.5-mm tall)

This eccentric figure, chipped from chert with web-like inclusions, is part of a cache of thirty-three from Guatemala, and one of seven that have faces chipped into them. The design is remarkably simple, and can readily be recognized as a snake with a face and a headdress. At first glance, there is nothing particularly remarkable about the figure, but continued examination reveals a host of interesting features. Iconographically, the snake image reminds us of a rattlesnake, and we know that the Pleiades asterism, or cluster of stars, was known to the Maya as tzab, the rattlesnake’s tail. Most cultures around the world ascribe seven stars to the Pleiades, but the count depends on viewing conditions and the observer’s visual acuity. The Pleiades can be occulted by the moon, and are obscured by the Sun around the first of June. Renewal of 52-year synchronization periods is marked by passage of the Pleiades directly overhead.

A key finding is that the figure has a hidden symmetry about its major axis. Proper orientation began with drawing grid lines parallel to the major axis and tangent to the figure, creating a bounding box. When an ellipse was generated in Photoshop©, it was tangent to the artifact outline in several places. Comparison with other artifacts shows that the rectangular frame is very common. Rather than being expressed in tangible form, it must be recognized indirectly. However, understanding the requirement for a squared frame allows an investigator to properly orient the artifact within the invisible bounding box. The ellipse constitutes a second virtual frame within the first, but symmetrically centered. As analysis has progressed, it appears that the virtual frames are used to express a symmetry not always readily apparent. Certainly the snake figure does not immediately appear symmetric.
Since seven visible stars are usually attributed to the Pleiades, a search was made for possible references to the number seven. Seven openings can be counted in the body, accompanied by seven body bulges. Sharp inflections of the head and tail also tally to seven.
Upon careful examination of the remaining eccentrics, it was seen that ellipses were often used. Based on the Pleiades example, it seems prudent to use the quadrilateral tangent to an ellipse extending beyond the physical frame of an artifact as the primary frame of reference.
Subtraction from a regular frame is used as a way to hide messages in plain sight. The ellipse is a common starting shape. By the time it becomes a scorpion or other figure, the ellipse foundation may be nearly unrecognizable. The rectangular frame surrounding the ellipse is even less obvious. In some cases, the remnants of the ellipse may constitute part of the message. For example, the seven sections of the Pleiades figure that touch the bounding ellipse (accounting for the broken nose) reinforce a message already conveyed in multiple ways. One function of an ellipse may be to preserve virtual symmetry, even though subtractions might appear to destroy visible symmetry. The use of tangent points to define bounding quadrilaterals minimizes the difficulties with achieving precision in chipped flint. It is much easier to position three to four edge points than to create perfectly straight lines in flint.
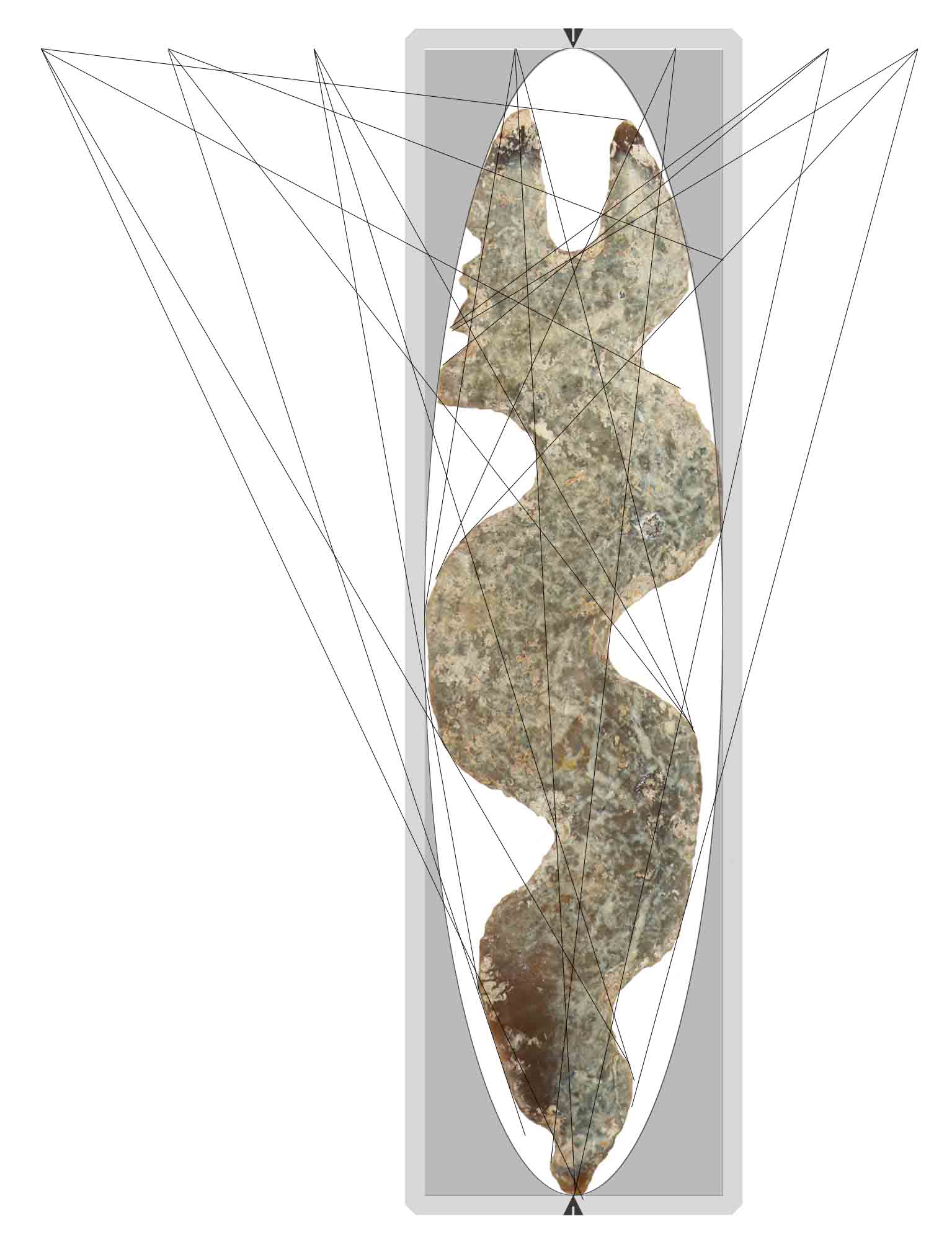
When lines were drawn tangent to body curves, it became evident that a series of planning points level with the top of the rectangular frame were used to guide the placement of the figure. Thus, the planning points validate using an ellipse to position the rectangular frame. Because the ellipse is a conic section, it has a unique shape relative to the width and length of the bounding rectangle.
Measuring the bounding rectangle perimeter and dividing by a standard unit of length (1.144-mm) derived statistically from similar measurements on the other 32 items cached with the snake figure produced a perimeter value of 343 units, or seven cubed.
Joining the upper planning points just outside the figure with the nadir point produced another perimeter of 343 units. The largest triangle measures 399 units, or seven times 57. Discarding the outer two planning points leaves a triangle with perimeter of 364 units, or seven times 52. The perimeters validate a standard of measure that was applied to composite sides of a perimeter figure, effectively compressing the dimension into a compact figure. Seldom do point-to-point measures reveal significant numbers, possibly to avoid confusion.
Other chert eccentrics are found to have alignments between features that redundantly reinforce the dead-center of the bounding rectangle. In this case, the dead-center can be found by connecting the outer planning points to where the 399-unit triangle cuts the far edge of the bounding rectangle. Such reinforcement seems to communicate that coincidences are by design.
By now, it should be apparent that Maya design contains much more than readily meets the eye. Keep in mind that very few examples have been subjected to this type of analysis. It is time to move beyond the language of glyphs to the language of geometry, where an untapped, rich feast of information waits.
